By now the process of analyzing and unpacking standards is familiar to most educators. In this era of standards-based instruction, unpacking standards to identify specific learning targets and underpinnings, then organizing those targets and underpinnings into a purposeful learning progression is almost ubiquitous. The goal, of course, is to create an intentional sequence through which learners advance from the simplest to the most sophisticated demonstrations of learning, with the most sophisticated typically being a demonstration of proficiency against the identified standard(s).
The unpacking of standards fuels the process of formative assessment. By unpacking and identifying specific targets, skills, and underpinnings, teachers are able to pinpoint aspects of strength and aspects in need of improvement. Since most standards are robust, complex, and include the combination of several elements, the unpacking process allows for a level of specificity in determining which skills are strong and which require further strengthening. The combination of unpacking and creating purposeful learning progressions makes it easier for teachers to determine why; why is the learner currently unsuccessful at performing at the expected level. Without this process, teachers can’t always be sure why learners are underperforming, while the learners themselves will never know. To accurately use assessment information formatively this process is essential.
With all of that, far too many teachers stop short of completing the process, which involves the repacking of standards when the verification of learning (summative assessment) is the primary purpose. Once a standard has been unpacked, the standard itself no longer exists unless the learners are asked to demonstrate their learning against the standard as a whole and not just the isolated skills that make up the standard. When it comes to meeting standards, the whole really is greater than the sum of its parts. A parallel can be drawn from cooking and the process we all go through to produce a meal. Let’s use a simple recipe – pancakes – combined with education terminology to illustrate the unpacking-repacking process.
If making pancakes is the goal, every recipe for pancakes has the ingredients separately identified. In other words, pancakes would have been unpacked to identify the specific ingredients necessary to produce the meal. But having the separate ingredients doesn’t make the meal; it’s the purposeful combination of the ingredients that produces the meal. Having flour, sugar, baking powder, eggs, milk, and vanilla on the counter doesn’t mean you have pancakes; the ingredients need to be combined with purpose. The random combination of ingredients will likely produce an undesirable outcome, but the purposeful (measured) combination of the ingredients brings breakfast magic! In other words, as much as pancakes need to be unpacked to identify the specific ingredients, the ingredients themselves need to be repacked to actually produce pancakes. Now let’s go back to the classroom with the image below to illustrate this point.
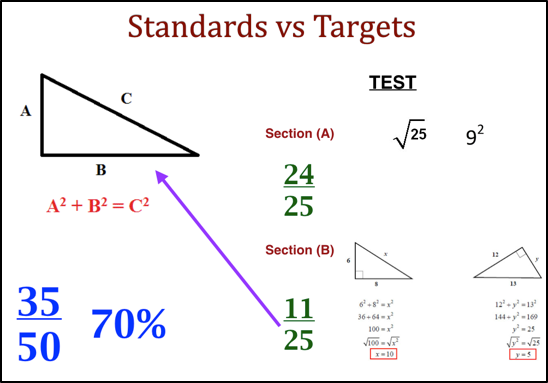
Imagine the standard a math teacher is teaching involves using the Pythagorean relationship (a2 + b2 = c2) to solve the third-side of a right triangle. The teacher dutifully unpacks the standard to identify the specific underpinnings, targets, and skills that support the meeting for the standard, which include knowing the formula, understanding the corresponding sides within the formula (i.e. “c” is always the hypotenuse), and most importantly, how to calculate squares and square roots. The teacher then masterfully creates a learning progression to develop these skills within each learner and uses assessments formatively to keep their learning on-track. Flash-forward to the end of the unit where it’s now time for the Pythagorean Relationship ‘test’ where the teacher will verify the meeting of the standard.
The test is made up of two sections. Section ‘A’ involves 25 questions where students are asked to calculate a simple square or square while section ‘B’ has 25 questions that involve using the Pythagorean relationship to solve the third-side of a right triangle when given the other two sides. Now imagine one learner earns a 24/25 on the first section, but only 11/25 on the second. Has this learner met the standard with any level of proficiency? No, of course not. However, if the teacher isn’t mindful, this test result could end up in the gradebook as a 35/50 (70%), even though it is obvious this student is nowhere near 70% proficient when it comes to solving the third-side of a right triangle. Even in a standards-based system, if not mindful, section 1 and 2 might be combined to come up with an overall proficiency level (i.e. 4 and 2 become 3). Of course, the potential combinations and complexities are more plentiful, but the point is that the teacher did not fully repack the standard for the summative purpose and, therefore, has a result that will skew the learner’s actual proficiency level against the standard. If it happens repeatedly it will undoubtedly distort the accuracy of the reported grade.
Understanding how to calculate squares and square roots does not mean learners can solve the third-side of a right triangle, but learners who can solve the third-side of a right triangle most certainly can calculate squares and square roots; it’s an underpinning inside the standard. Hypothetically (and admittedly a far less likely scenario) imagine the test result in reverse where the learner scores 11/25 on the first section as a result of silly mistakes, but puts it all together in the second section and scores 24/25. Is 70% or ‘3’ accurate in terms of the learner meeting the standard? The failure to repack standards can have real consequences for both teachers and learners when it comes to the accurate reporting of achievement. For teachers, the verification of learning can be distorted and artificially lengthy (the first section on the test is unnecessary). For learners, their grades or levels can inaccurately communicate where they are in relation to the standards, setting them up for a potential rude awakening should an external, standardized test be part of the process. The learner could potentially think he or she is proficient with using the Pythagorean formula and, therefore, settle instead of investing in further learning.
The potential combinations and results are too plentiful to outline in one post, but the point is that unpacking standards serves a real purpose in the instructional paradigm, but the failure to repack can have real consequences. Skills in isolation are developed, but performances usually involve the combination of aspects, skills, and elements into a more sophisticated demonstration. Volleyball players must combine the toss, contact point, footwork, weight transfer, and follow-through to serve effectively; one of these skills in isolation doesn’t equate to an effective serve. Understanding the definition of the three types of irony doesn’t mean a learner can correctly identify the specific type of irony within a piece of literature or write their own original piece involving, say, situational irony.
To be clear, all of the skills, underpinnings, and targets need to be assessed, but they need to be assessed formatively and used exclusively for the purpose of instruction and feedback. The verification of the meeting of standards needs to be about the meeting of standards. In doing so, teachers will be clearer about what assessment results represent and will be better prepared to accurately interpret and respond to results in ways that support the students’ positive growth trajectory.


I was searching for some updated links on unpacking standards and came across your link on “repacking”. I have done repacking before as a teacher and math curriculum specialist but I did not have a catch-all term to describe it. Thank you for that terminology. I appreciate it.